Familias de politopos
Hay varias familias de politopos simétricos con simetría irreducible que tienen un miembro en más de una dimensionalidad. Aquí se tabulan con los gráficos de proyección de sus polígonos de Petrie y con sus diagramas de Coxeter-Dynkin:
| Tabla de familias de politopos irreducibles | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Familia n |
n-símplex | n-hipercubo | n-politopo de cruce | n-demicubo | 1k2 | 2k1 | k21 | Politopo pentagonal | ||||||||
| Grupo | An | Bn |
|
|
Hn | |||||||||||
| 2 |  |
 |
 p-gono (ejemplo: p=7) |
 Hexágono |
 Pentágono | |||||||||||
| 3 |  Tetraedro |
 Cubo |
 Octaedro |
 Tetraedro |
 Dodecaedro |
 Icosaedro | ||||||||||
| 4 | 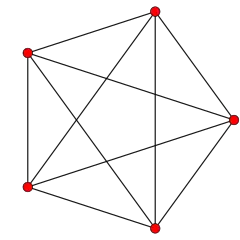 Pentácoron |
 |
 Hexadecacoron |
 |
 Icositetracoron |
 Hecatonicosacoron |
 Hexacosicoron | |||||||||
| 5 |  5-símplex |
 Penteracto |
 5-ortoplex |
 5-demicubo |
||||||||||||
| 6 |  6-símplex |
 Hexeracto |
 6-ortoplex |
 6-demicubo |
 122 |
 221 |
||||||||||
| 7 |  7-símplex |
 Hepteracto |
 7-ortoplex |
 7-demicubo |
 132 |
 231 |
 321 |
|||||||||
| 8 |  8-símplex |
 Octoracto |
 8-ortoplex |
 8-demicubo |
 142 |
 241 |
 421 |
|||||||||
| 9 |  9-símplex |
 Eneracto |
 9-ortoplex |
 9-demicubo |
||||||||||||
| 10 |  10-símplex |
 decaracto |
 10-ortoplex |
 10-demicubo |
||||||||||||
| Politopos regulares y uniformes convexos fundamentales en las dimensiones 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Familia | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Polígono regular | Triángulo | Cuadrado | p-gono | Hexágono | Pentágono | |||||||
| Poliedro uniforme | Tetraedro | Octaedro • Cubo | Demicubo | Dodecaedro • Icosaedro | ||||||||
| 4-politopo uniforme | Pentácoron | Hexadecacoron • Teseracto | Demiteseracto | Icositetracoron | Hecatonicosacoron • Hexacosicoron | |||||||
| 5-politopo uniforme | 5-símplex | 5-ortoplex • Penteracto | 5-demicubo | |||||||||
| 6-politopo uniforme | 6-símplex | 6-ortoplex • Hexeracto | 6-demicubo | 122 • 221 | ||||||||
| 7-politopo uniforme | 7-símplex | 7-ortoplex • Hepteracto | 7-demicubo | 132 • 231 • 321 | ||||||||
| 8-politopo uniforme | 8-símplex | 8-ortoplex • Octoracto | 8-demicubo | 142 • 241 • 421 | ||||||||
| 9-politopo uniforme | 9-símplex | 9-ortoplex • Eneracto | 9-demicubo | |||||||||
| 10-politopo uniforme | 10-símplex | 10-ortoplex • Decaracto | 10-demicubo | |||||||||
| n-politopo uniforme | n-símplex | n-ortoplex • n-cubo | n-demicubo | 1k2 • 2k1 • k21 | n-politopo pentagonal | |||||||
| Relacionados: Familias de politopos • Politopo regular • Anexo:Politopos regulares y compuestos | ||||||||||||
Este artículo ha sido escrito por Wikipedia. El texto está disponible bajo la licencia Creative Commons - Atribución - CompartirIgual. Pueden aplicarse cláusulas adicionales a los archivos multimedia.