Romboide

El nombre romboide proviene del latín tardío rhomboides, y este del griego ρομβοειδής, leído [romboeides], de ρόμβoς (rombo) y -ειδής (tener el parecido).[1]

Un romboide posee las siguientes propiedades:

• Tiene dos pares de lados opuestos, iguales y paralelos entre sí.
• Cada par de ángulos contiguos son suplementarios.
• Tiene dos ángulos agudos y dos obtusos.
• Las bisectrices de los ángulos contiguos son perpendiculares entre sí.
• El punto común a las dos diagonales es centro de simetría central.[5]
• Como en todo polígono de cuatro lados, la suma de todos sus ángulos interiores es igual a 360°.
• Las diagonales se bisecan mutuamente en un punto llamado baricentro.
• La diagonal mayor determina sobre el romboide dos triángulos obtusángulos congruentes.

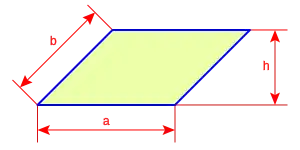
Considerando el romboide de lados a y b, y de altura h respecto al lado a, llamado base, se pueden determinar las siguientes medidas:

El perímetro de un romboide es:

${\displaystyle P=2\,(a+b)}$

Que es la suma de las medidas de todos los lados.

El área se obtiene multiplicando la longitud de un lado, ${\displaystyle a}$, por la distancia al lado opuesto, ${\displaystyle h}$:

${\displaystyle S=a\cdot h}$

${\displaystyle S=a\cdot b\cdot \operatorname {sen} \alpha }$, siendo α el ángulo interior entre los lados a y b

• Cuadrado
• Rombo
• Rectángulo
• Deltoide
• Trapecio
• Trapezoide
• Paralelogramo