Ciencias formales

La matemática[3] (del latín mathematĭca, y este del griego μαθηματικά, transliterado como mathēmatiká, derivado de μάθημα, tr. máthēma. 'conocimiento') es una ciencia formal que, partiendo de axiomas y siguiendo el razonamiento lógico, estudia las propiedades, estructuras abstractas y relaciones entre entidades abstractas como números, figuras geométricas, iconos, glifos o símbolos en general.^{[cita requerida]}

La matemática es un conjunto de lenguajes formales que pueden usarse como herramienta para plantear problemas en contextos específicos. Por ejemplo, el siguiente enunciado puede expresarse de dos formas: X es mayor que Y y Y es mayor que Z, o en forma simplificada puede decirse que X > Y > Z. Este es el motivo por el cual las matemáticas son tan solo un lenguaje simplificado con una herramienta para cada problema específico (por ejemplo, 2 × 2 = 4 o bien 2 + 2 = 4).^{[cita requerida]}

Las ciencias naturales han hecho un uso extensivo de la matemática para explicar diversos fenómenos observables, tal como lo expresó Eugene Paul Wigner (Premio Nobel de Física en 1963):[4]

La enorme utilidad de la matemática en las ciencias naturales es algo que roza lo misterioso, y no hay explicación para ello. No es en absoluto natural que existan «leyes de la naturaleza», y mucho menos que el hombre sea capaz de descubrirlas. El milagro de lo apropiado que resulta el lenguaje de las matemáticas para la formulación de las leyes de la física es un regalo maravilloso que no comprendemos ni nos merecemos.

Galileo Galilei, en la misma línea, lo había expresado así: «La matemática es el lenguaje en el que Dios escribió el universo.»

Mediante la abstracción y el uso de la lógica en el razonamiento, la matemática ha evolucionado basándose en el cálculo y las mediciones, junto con el estudio sistemático de la forma y el movimiento de los objetos físicos. Las matemáticas, desde sus comienzos, han tenido un fin práctico.

Las explicaciones que se apoyaban en la lógica aparecieron por primera vez con la matemática helénica, especialmente con los Elementos de Euclides. La matemática siguió desarrollándose, con continuas interrupciones, hasta que en el Renacimiento las innovaciones matemáticas interactuaron con los nuevos descubrimientos científicos. Como consecuencia, hubo una aceleración en la investigación que continúa hasta la actualidad.

Hoy día, la matemática se usa en todo el mundo como una herramienta esencial en muchos campos, entre los que se encuentran las ciencias naturales, la ciencias aplicadas, las humanidades, la medicina y las ciencias sociales, e incluso disciplinas que, aparentemente, no están vinculadas con ella, como la música (por ejemplo, en cuestiones de resonancia armónica). Las matemáticas aplicadas, rama de la matemática destinada a la aplicación del conocimiento matemático a otros ámbitos, inspiran y hacen uso de los nuevos descubrimientos matemáticos y, en ocasiones, conducen al desarrollo de nuevas disciplinas. Los matemáticos también participan en la matemática pura, sin tener en cuenta la aplicación de esta ciencia, aunque las aplicaciones prácticas de la matemática pura suele ser descubiertas con el paso del tiempo.

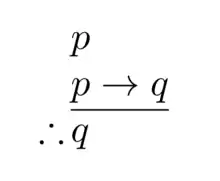
La lógica es una rama de la filosofía[5] de carácter interdisciplinario, entendida como la ciencia formal que estudia los principios de la demostración y la inferencia válida,[6] las falacias, las paradojas y la noción de verdad.[7]

La lógica se divide en varias categorías según su campo de estudio. La lógica filosófica estudia el concepto y la definición, la enunciación o proposición y la argumentación utilizando los métodos y resultados de la lógica moderna para el estudio de problemas filosóficos. La lógica matemática estudia la inferencia mediante sistemas formales como la lógica proposicional, la lógica de primer orden y la lógica modal. La lógica informal se enfoca en el desarrollo lingüístico de los razonamientos y sus falacias. La lógica computacional es la aplicación de la lógica matemática a las ciencias de la computación.

Los orígenes de la lógica se remontan a la Edad Antigua, con brotes independientes en China, India y Grecia. Desde entonces, la lógica tradicionalmente se considera una rama de la filosofía, pero en el siglo XX la lógica ha pasado a ser principalmente la lógica matemática, y por lo tanto ahora también se considera parte de las matemáticas, e incluso una ciencia formal independiente.

No existe un acuerdo universal sobre la definición exacta o los límites de la lógica.[8][9][10] Sin embargo, el ámbito de la lógica (interpretada en sentido amplio) incluye:

• La clasificación de los argumentos.
• El análisis sistemático de las formas lógicas.
• El estudio sistemático de la validez de las inferencias deductivas.
• La fuerza de las inferencias inductivas.
• El estudio de los argumentos defectuosos, como las falacias.
• El estudio de las paradojas lógicas.
• El estudio de la sintaxis y la semántica de los lenguajes formales.
• El estudio de los conceptos de sentido, denotación y verdad.

Históricamente, la lógica se ha estudiado principalmente en filosofía desde la antigüedad, en matemáticas desde mediados del siglo XIX y en informática desde mediados del siglo XX. Más recientemente, la lógica también se ha estudiado en lingüística y en ciencias cognitivas. En general, la lógica sigue siendo un área de estudio fuertemente interdisciplinaria.

Las ciencias de la computación o ciencias de la informática son las ciencias formales que abarcan las bases teóricas de la información y la computación, así como su aplicación en sistemas computacionales.[11][12][13] El cuerpo de conocimiento de las ciencias de la computación es frecuentemente descrito como el estudio sistemático de los procesos algorítmicos que describen y transforman información: su teoría, análisis, diseño, eficiencia, implementación, algoritmos sistematizados y aplicación.[14] En términos más específicos se trata del estudio sistemático de la factibilidad, estructura, expresión y mecanización de procedimientos metódicos (o algoritmos) que subyacen en la adquisición, representación, procesamiento, almacenamiento, comunicación y acceso a la información. La información puede estar codificada en forma de bits en una memoria de computadora, o en algún otro objeto, como los genes y proteínas en una célula biológica.[15]

Existen diversas ramas o disciplinas dentro de las ciencias de la computación; algunos resaltan los resultados específicos del cómputo (como los gráficos por computadora), mientras que otros (como la teoría de la complejidad computacional) se relacionan con propiedades de los algoritmos usados al realizar cómputo; y otros se enfocan en los problemas que requieren la implementación de sistemas computacionales. Por ejemplo, los estudios de la teoría de lenguajes de programación describen un cómputo, mientras que la programación de computadoras aplica lenguajes de programación específicos para desarrollar una solución a un problema computacional específico. Un computólogo se especializa en teoría de la computación y en el diseño e implementación de sistemas computacionales.[16]

Según Peter J. Denning, la cuestión fundamental en que se basa la ciencia de la computación es: «¿Qué puede ser (eficientemente) automatizado?».[17]