Álgebra de conjuntos

Un conjunto es una colección de objetos considerada como un objeto en sí. Un conjunto está definido únicamente por los elementos que lo componen, y no por la manera en la que se lo representa.

Existe una serie de relaciones básicas entre conjuntos y sus elementos:

• Pertenencia. La relación relativa a conjuntos más básica es la relación de pertenencia. Dado un elemento ${\displaystyle x}$, este puede o no pertenecer a un conjunto dado ${\displaystyle A}$. Esto se indica como:

${\displaystyle x\in A\quad \longrightarrow }$ ${\displaystyle x}$ pertenece a ${\displaystyle A}$.

${\displaystyle x\notin A\quad \longrightarrow }$ ${\displaystyle x}$ no pertenece a ${\displaystyle A}$.

• Igualdad. Dos conjuntos son iguales si y solo si tienen los mismos elementos. Este principio, denominado principio de extensionalidad establece el hecho de que un conjunto queda definido únicamente por sus elementos

${\displaystyle A=B\quad \longrightarrow }$ ${\displaystyle A}$ es igual a ${\displaystyle B}$.

${\displaystyle A\neq B\quad \longrightarrow }$ ${\displaystyle A}$ no es igual a ${\displaystyle B}$.

• Inclusión. Dado un conjunto ${\displaystyle A}$, subcolección del conjunto ${\displaystyle B}$ o igual a este, sus elementos son un subconjunto de ${\displaystyle B}$, y se indica como:

${\displaystyle A\subseteq B\quad \longrightarrow }$ ${\displaystyle A}$ es un subconjunto de ${\displaystyle B}$.

${\displaystyle A\nsubseteq B\quad \longrightarrow }$ ${\displaystyle A}$ no es subconjunto de ${\displaystyle B}$.

El conjunto vacío es el conjunto sin ningún elemento, y se denota por ∅ o por ${\displaystyle \{\}}$. El conjunto universal es el conjunto que contiene todos los elementos posibles, dentro del contexto considerado. Por ejemplo, si se estudian los números naturales, el conjunto universal es el conjunto de todos ellos, ${\displaystyle \mathbb {N} }$. De manera general, el conjunto universal se denota por ${\displaystyle U}$.

Ejemplos

• Cada número natural es elemento del conjunto ${\displaystyle \mathbb {N} =\{1,2,3,\dots ,n\}}$ de los números naturales: ${\displaystyle 1\in \mathbb {N} ,2\in \mathbb {N} ,3\in \mathbb {N,\dots ,n\in \mathbb {N} } }$. Cada número par es también un número natural, por lo que el conjunto ${\displaystyle \mathbb {P} }$ de los números pares, ${\displaystyle P=\{2,4,6,\dots ,2n\},n\in \mathbb {N} }$, es un subconjunto de ${\displaystyle \mathbb {N} }$: ${\displaystyle P\subseteq \mathbb {N} }$.
• Dado el conjunto de letras ${\displaystyle V=\{o,i,e,u,a\}}$, se cumple por ejemplo que ${\displaystyle a\in V}$ o también ${\displaystyle i\in V}$. El conjunto de letras ${\displaystyle U=\{{\text{vocales del español}}\}}$ contiene los mismos elementos que ${\displaystyle V}$, por lo que ambos conjuntos son iguales, ${\displaystyle V=U}$.

Operaciones con conjuntos

Unión

Intersección

Diferencia

Complemento

Diferencia simétrica

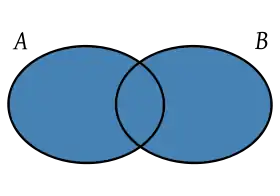
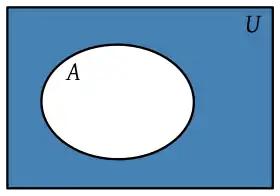
Las operaciones básicas del álgebra de conjuntos son:

• Unión. La unión de dos conjuntos A y B es el conjunto A ∪ B que contiene todos los elementos de A y de B.
• Intersección. La intersección de dos conjuntos A y B es el conjunto A ∩ B que contiene todos los elementos comunes de A y B.
• Diferencia. La diferencia entre dos conjuntos A y B es el conjunto A \ B que contiene todos los elementos de A que no pertenecen a B.
• Diferencia simétrica. La diferencia simétrica entre dos conjuntos A y B es el conjunto que contiene los elementos de A y B que no son comunes.
• Complemento. El complemento de un conjunto A es el conjunto A^∁ que contiene todos los elementos que no pertenecen a A.
• Producto cartesiano. El producto cartesiano de dos conjuntos A y B es el conjunto A × B que contiene todos los pares ordenados (a, b) cuyo primer elemento pertenece a A y su segundo elemento pertenece a B.

• Teoría de conjuntos
• Teoría axiomática de conjuntos
• Álgebra de Boole
• Dinámica de sistemas