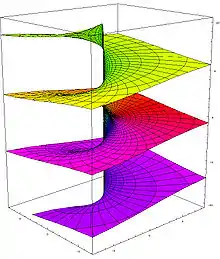
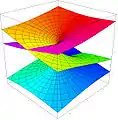
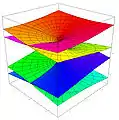
Superficie de Riemann
En geometría algebraica, una superficie de Riemann es una variedad compleja de dimensión (compleja) uno. Consecuentemente, la variedad real subyacente será de dimensión 2.
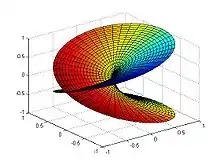
Historia
El desarrollo de la idea de superficie de Riemann comenzó a mediados del siglo XIX de la mano del matemático Bernhard Riemann, con los intentos de extender el dominio de definición de funciones analíticas definidas sobre un abierto U del plano complejo. La extensión maximal (extensión analítica) se lograba no sobre el propio plano complejo, sino sobre copias de abiertos del mismo que se solapaban, en lo que hoy día conocemos como variedad compleja de dimensión uno.
Concepto
Una variedad real de dimensión 2 puede convertirse en una superficie de Riemann (frecuentemente de varios modos no equivalentes) si y solo si es orientable. De este modo, la esfera y el toro admitirán estructuras complejas, pero la banda de Möbius, la botella de Klein y el plano proyectivo real no.
Se sabe que la 2-esfera tiene una sola estructura analítica. Mientras que cada superficie orientable de género mayor que cero tiene una infinidad, contrastando con el punto de vista diferenciable ya que las superficies sólo tienen una estructura diferenciable.
Las superficies de Riemann constituyen el lugar natural donde estudiar el comportamiento global de numerosas funciones. P ej:
Ejemplos
- Sea S = C ∪ {∞} y sea f(z) = z donde z pertenece a S \ {∞} y g(z) = 1 / z donde z pertenece a S \ {0} y 1/∞ se define como 0. Así definidas, f y g son cartas complejas compatibles, y { f, g } es un atlas para S, convirtiendo a S en una superficie de Riemann compacta llamada la esfera de Riemann.
- Sea G un grupo de biholomorfismos de una superficie de Riemann , que actúa de modo libre y propiamente discontinuo, entonces el espacio cociente es una superficie de Riemann y la proyección p: es una aplicación recubridora.
- Por ejemplo, puede ser un grupo de traslaciones del plano complejo,. Sea el grupo generado por dos traslaciones independientes, por ejemplo:
- donde a es un número complejo no real. El espacio cociente será homeomorfo al toro, La topología no dependerá de la elección de a (es siempre un toro), pero la estructura compleja cambia sensiblemente al variar a.
- Numerosos ejemplos de superficies de Riemann no compactas se obtienen por el procedimiento de extensión analítica.
Funciones
Toda superficie de Riemann no compacta admite funciones holomorfas no constantes.
Esto contrasta con que en una superficie de Riemann compacta toda función holomorfa es constante debido al principio del máximo. Sin embargo, en superficies compactas siempre existirán funciones meromorfas no constantes, que pueden considerarse como aplicaciones holomorfas de la superficie sobre la esfera de Riemann C ∪ {∞}).
Clasificación de superficies de Riemann
El conjunto de superficies de Riemann puede dividirse en tres tipos: las superficies hiperbólicas, las parabólicas y las elípticas. Esta división viene dada por el teorema de uniformización, que garantiza que toda superficie de Riemann simplemente conexa es conformemente equivalente a una de las siguientes:
- al plano complejo
- a la esfera de Rieman , también llamada línea proyectiva compleja o
- al disco abierto D := {z ∈ C : |z| < 1} o a la superficie equivalente formada por el semiplano superior H := {z ∈ C : Im(z) > 0}.
En caso de que la superficie X no sea simplemente conexa, podremos afirmar que su recubridor universal Y es conformemente equivalente a uno de los tres modelos anteriores. En ese caso, la superficie X podrá obetenersese como el espacio cociente de Y bajo la acción de un grupo de biholomorfismos del recubridor Y que actúe de modo libre (es decir, sin puntos fijos) y propiamente discontinuo.
- Cocientes de la esfera (superficies elípticas). Los biholomorfismos de la esfera son exactamente las transformaciones de Moebius. Como una transformación de Moebius siempre deja un punto fijo, no obtendremos ningún cociente de la esfera.
- Cocientes del plano (superficies parabólicas). Los biholomorfismos del plano complejo que actúan de modo libre y propiamente discontinuo son las traslaciones, en concreto los grupos de traslaciones con uno o dos generadores, isomorfos a o a . Los cocientes respectivos son topológicamente equivalentes a una corona circular o a un toro. Al ser las traslaciones isometrías respecto de la métrica plana del plano, inducen una métrica plana en el cociente.
- Cocientes del disco (superficies hiperbólicas)
Un grupo de biholomorfismos del disco que actúe de modo libre y propiamente discontinuo se dice un grupo Fuchsiano. Existen numerosos grupos Fuchsianos, y su estudio es un ramo importante de la geometría moderna.
Como todo biholomorfismo del disco resulta ser una isometría de la métrica hiperbólica del disco unidad, también conocida como métrica de Poincaré, se induce una métrica hiperbólica en el cociente.
Clasificación teórica de funciones
El esquema de clasificación anterior suele ser utilizado por los geómetras. Existe una clasificación diferente para las superficies de Riemann que suelen utilizar los analistas complejos. Emplea una definición diferente para "parabólico" e "hiperbólico". En este esquema de clasificación alternativo, una superficie de Riemann se denomina "parabólica" si no hay funciones subarmónicas negativas no constantes en la superficie y, de lo contrario, se denomina "hiperbólica".[1][2] Esta clase de superficies hiperbólicas se subdivide en subclases según si los espacios de funciones distintos de las funciones subarmónicas negativas están degenerados, por ejemplo las superficies de Riemann en las que todas las funciones holomorfas acotadas son constantes, o en las que todas las funciones armónicas acotadas son constantes, o en las que todas las funciones armónicas positivas son constantes, etc.
Para evitar confusiones, la clasificación basada en métricas de curvatura constante se llama clasificación geométrica, y la basada en la degeneración de los espacios de funciones, clasificación función-teórica. Por ejemplo, la superficie de Riemann que consta de "todos los números complejos excepto el 0 y el 1" es parabólica en la clasificación de teoría de funciones pero es hiperbólica en la clasificación geométrica.
Referencias
- Ahlfors, Lars; Sario, Leo (1960), Riemann Surfaces (1st edición), Princeton, New Jersey: Princeton University Press, p. 204.
- Rodin, Burton; Sario, Leo (1968), Principal Functions (1st edición), Princeton, New Jersey: D. Von Nostrand Company, Inc., p. 199, ISBN 9781468480382.
Fuentes
- Farkas, Hershel M.; Kra, Irwin (1980), Riemann Surfaces (2nd edición), Berlin, New York: Springer-Verlag, ISBN 978-0-387-90465-8.
- Pablo Arés Gastesi, Riemann Surfaces Book.
- Hartshorne, Robin (1977), Algebraic Geometry, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90244-9, MR 0463157, OCLC 13348052., esp. chapter IV.
- Jost, Jürgen (2006), Compact Riemann Surfaces, Berlin, New York: Springer-Verlag, pp. 208-219, ISBN 978-3-540-33065-3.
- Papadopoulos, Athanase, ed. (2007), Handbook of Teichmüller theory. Vol. I, IRMA Lectures in Mathematics and Theoretical Physics 11, European Mathematical Society (EMS), Zürich, ISBN 978-3-03719-029-6, MR 2284826, S2CID 119593165, doi:10.4171/029.
- Lawton, Sean; Peterson, Elisha (2009), Papadopoulos, Athanase, ed., Handbook of Teichmüller theory. Vol. II, IRMA Lectures in Mathematics and Theoretical Physics 13, European Mathematical Society (EMS), Zürich, ISBN 978-3-03719-055-5, MR 2524085, S2CID 16687772, arXiv:math/0511271, doi:10.4171/055.
- Papadopoulos, Athanase, ed. (2012), Handbook of Teichmüller theory. Vol. III, IRMA Lectures in Mathematics and Theoretical Physics 19, European Mathematical Society (EMS), Zürich, ISBN 978-3-03719-103-3, doi:10.4171/103.
- *Remmert, Reinhold (1998). «From Riemann Surfaces to Complex Spaces». Séminaires et Congrès. Zbl 1044.01520.
- Siegel, Carl Ludwig (1955), «Meromorphe Funktionen auf kompakten analytischen Mannigfaltigkeiten», Nachrichten der Akademie der Wissenschaften in Göttingen. II. Mathematisch-Physikalische Klasse 1955: 71-77, ISSN 0065-5295, MR 0074061.
- Weyl, Hermann (2009) [1913], The concept of a Riemann surface (3rd edición), New York: Dover Publications, ISBN 978-0-486-47004-7, MR 0069903.
Enlaces externos
- Hazewinkel, Michiel, ed. (2001), «Riemann surface», Encyclopaedia of Mathematics (en inglés), Springer, ISBN 978-1556080104.
- McMullen, C. «Complex Analysis on Riemann Surfaces Math 213b». Harvard Math. Harvard University.