Mediana (estadística)

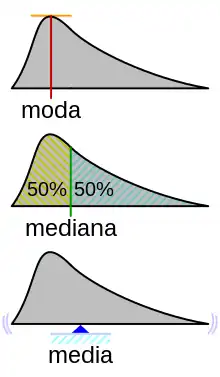
En teoría de la probabilidad, se define la mediana de una variable aleatoria como un número tal que la variable tiene igual probabilidad de tomar valores menores o mayores que él. Finalmente, en inferencia estadística se estudia la mediana poblacional y la mediana muestral.

La mediana se utiliza normalmente para dar un valor "típico" que caracteriza un conjunto de datos. En comparación con la media, la propiedad esencial de la mediana es que no se ve afectada si hay un grupo de datos mucho más pequeño o mucho más grandes que las otras, mientras que la media sí que puede quedar distorsionada. Un ejemplo de esta situación se da al analizar el tiempo que los estudiantes universitarios tardan en acabar una carrera, el hecho que haya algunos estudiantes que estén muchos años para acabar la carrera (porque se ponen a trabajar y retardan los estudios, u otros motivos) hace que la media no refleje bien los datos; al contrario, la mediana no es sensible a estos valores extremos, y proporciona un mejor valor representativo de la duración de los estudios.

Existen dos métodos para el cálculo de la mediana:

1. Considerando los datos en forma individual, sin agruparlos.
2. Utilizando los datos agrupados en intervalos de clase.

Sean ${\displaystyle x_{1},x_{2},x_{3},\ldots ,x_{n}}$ los datos de una muestra ordenada en orden creciente y designando la mediana como ${\displaystyle M_{e}}$, distinguimos dos casos:

a) Si n es impar, la mediana es el valor que ocupa la posición ${\displaystyle (n+1)/2}$ una vez que los datos han sido ordenados (en orden creciente o decreciente), porque este es el valor central. Es decir: ${\displaystyle M_{e}=x_{(n+1)/2}}$.

Por ejemplo, si tenemos 5 datos, que ordenados son: ${\displaystyle x_{1}=3}$, ${\displaystyle x_{2}=6}$, ${\displaystyle x_{3}=7}$, ${\displaystyle x_{4}=8}$, ${\displaystyle x_{5}=9}$ => El valor central es el tercero: ${\displaystyle x_{(5+1)/2}=x_{3}=7}$. Este valor, que es la mediana de ese conjunto de datos, deja dos datos por debajo (${\displaystyle x_{1}}$, ${\displaystyle x_{2}}$) y otros dos por encima de él (${\displaystyle x_{4}}$, ${\displaystyle x_{5}}$).

b) Si n es par, la mediana es la media aritmética de los dos valores centrales. Cuando ${\displaystyle n}$ es par, los dos datos que están en el centro de la muestra ocupan las posiciones ${\displaystyle n/2}$ y ${\displaystyle (n/2)+1}$. Es decir: ${\displaystyle M_{e}=(x_{\frac {n}{2}}+x_{{\frac {n}{2}}+1})/2}$.

Por ejemplo, si tenemos 6 datos, que ordenados son: ${\displaystyle x_{1}=3}$, ${\displaystyle x_{2}=6}$, ${\displaystyle x_{3}=7}$, ${\displaystyle x_{4}=8}$, ${\displaystyle x_{5}=9}$, ${\displaystyle x_{6}=10}$. Hay dos valores que están por debajo del ${\displaystyle x_{\frac {6}{2}}=x_{3}=7}$ y otros dos que quedan por encima del siguiente dato ${\displaystyle x_{{\frac {6}{2}}+1}=x_{4}=8}$. Por tanto, la mediana de este grupo de datos es la media aritmética de estos dos datos: ${\displaystyle M_{e}={\frac {x_{3}+x_{4}}{2}}={\frac {7+8}{2}}=7,5}$.

Al tratar con datos agrupados en intervalos, si ${\displaystyle {\frac {n}{2}}}$ coincide con el valor de una frecuencia acumulada, el valor de la mediana coincidirá con la abscisa correspondiente. Si no coincide con el valor de ninguna abscisa, se calcula a través de semejanza de triángulos en el histograma o polígono de frecuencias acumuladas, utilizando la siguiente equivalencia:

${\displaystyle {\frac {N_{i}-N_{i-1}}{a_{i}-a_{i-1}}}={\frac {{\frac {n}{2}}-N_{i-1}}{p}}\Rightarrow p={\frac {{\frac {n}{2}}-N_{i-1}}{N_{i}-N_{i-1}}}(a_{i}-a_{i-1})}$

Donde ${\displaystyle N_{i}}$ y ${\displaystyle N_{i-1}}$ son las frecuencias absolutas acumuladas tales que ${\displaystyle N_{i-1}<{\frac {n}{2}}<N_{i}}$, ${\displaystyle a_{i-1}}$ y ${\displaystyle a_{i}}$ son los extremos, interior y exterior, del intervalo donde se alcanza la mediana y ${\displaystyle M_{e}=a_{i-1}+p}$ es la abscisa a calcular, la mediana. Se observa que ${\displaystyle a_{i}-a_{i-1}}$ es la amplitud de los intervalos seleccionados para el diagrama.

xi	fi	Ni
[x11-x12]	f1	N1
.	.	.
.	.	.
.	.	N(i-2)
[x(i-1)1-x(i-1)2]	f(i-1)	f(i-1)+N(i-2)=${\displaystyle N_{i-1}}$
[xi1-xi2]	${\displaystyle f_{i}}$	fi+Ni-1=Ni
[x(i+1)1-x(i+1)2]	f(i+1)	f(i+1)+Ni=N(i+1)
.	.	.
.	.	.
.	.
[xM1-xM2]	fM	fM+N(M-1)=NM

Consideramos:

- x₁₁ valor mínimo< Entonces:

${\displaystyle Mediana=x_{i1}+\left({\cfrac {(N_{M}/2)-N_{i-1}}{f_{i}}}\right).(x_{i2}-x_{i1})}$

donde:

${\displaystyle x_{i1}}$ = es el límite inferior de la clase de la mediana.

${\displaystyle \left({\cfrac {N_{M}}{2}}\right)}$ = es la posición de la mediana.

${\displaystyle N_{i-1}}$ = es la frecuencia acumulada de la clase premediana.

${\displaystyle f_{i}}$ = es la frecuencia absoluta de la clase de la mediana.

${\displaystyle (x_{i2}-x_{i1})}$ = ${\displaystyle A_{i}}$ = Amplitud del intervalo de la clase de la mediana.

• Desviación estándar
• Frecuencia
• Moda (estadística)
• Media (matemáticas)
• Media aritmética o promedio
• Parámetro estadístico
• Valor esperado

• Simulación de la mediana de una variable discreta con R (lenguaje de programación)

• Weisstein, Eric W., «Statistical Median» a MathWorld (en ingles).
• Sheskin, David (27 de agosto de 2003). Handbook of parametric and nonparametric statistical procedures (en inglés) (3rd edición). Boca Raton: Chapman & Hall/CRC. pp. 7-. ISBN 978-1-4200-3626-8.
• Bissell, Derek (1994). Statistical methods for SPC and TQM (en inglés) (1st edición). London: Chapman & Hall. pp. 26-. ISBN 978-0-412-39440-9.
• Lobez Urquia, J., Casa Aruta, E.. Estadística intermedia. Segunda edición. Barcelona: Vicens-Vives, 1975, p. 43.
• Moore, David S. (1995). Estadística aplicada básica. Barcelona: Antonio Bosch. ISBN 8485855809.
• Loeve, Michel. Teoría de la probabilidad. Madrid: Tecnos. p. 238. ISBN 8430906630.
• Serfling, Robert J. (2009). Approximation theorems of mathematical statistics (en inglés). New York: Wiley. pp. 74-77. ISBN 1282307479.
• DeGroot, Morris H. (1931, 1988). Probabilidad y estadística (2a. edición). Wilmington, Delawere, E.U.A.: Addison-Wesley Iberoamericaca. ISBN 0201644053.