Demostración sin palabras

Una prueba sin palabras para el teorema de la suma de los números impares.

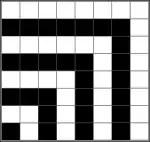
La afirmación de que la suma de todos los números impares positivos hasta 2n − 1 es un cuadrado; más específicamente, el cuadrado perfecto n², se puede demostrar con una prueba sin palabras, como se muestra a la derecha.[3] El primer cuadrado está formado por 1 bloque; 1 es el primer cuadrado. La siguiente tira, hecha de cuadrados blancos, muestra cómo agregar 3 bloques más forma otro cuadrado: cuatro. La siguiente tira, hecha de cuadrados negros, muestra cómo agregar 5 bloques más forma el siguiente cuadrado. Este proceso puede continuarse indefinidamente.

Una prueba sin palabras para el teorema de Pitágoras incluida en el Zhoubi Suanjing.

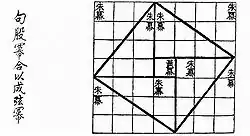
El Teorema de Pitágoras puede probarse sin palabras, como se muestra en el segundo diagrama a la izquierda. Los dos métodos diferentes para determinar el área del cuadrado grande dan la relación

${\displaystyle a^{2}+b^{2}=c^{2}}$

entre los lados. Esta prueba es más sutil que la anterior, pero aún puede considerarse una prueba sin palabras.[4]

Una prueba gráfica de la desigualdad de Jensen.

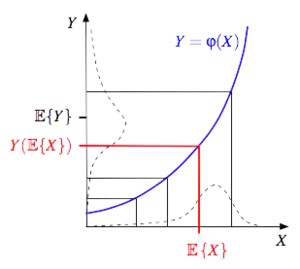
La desigualdad de Jensen también se puede demostrar gráficamente, como se ilustra en el tercer diagrama. La curva de trazos en el eje "X" es la distribución hipotética de "X", mientras que la curva a trazos sobre el eje "Y" es la distribución correspondiente de los valores de "Y". Nótese que la aplicación convexa Y (X) cada vez se "estira" más con el incremento de los valores de X en la distribución.[5]