Nudo de trébol
Plantilla:Short description Plantilla:About Plantilla:Infobox Teoría del nudo En la Teoría de nudos, una rama de las Matemáticas, el nudo de trébol es el ejemplo más simple de un nudo no trivial. El trébol se puede obtener uniendo los dos extremos sueltos de un nudo simple común, dando como resultado un lazo anudado. Como el nudo más simple, el trébol es fundamental para el estudio de la teoría matemática del nudo.
El nudo del trébol lleva el nombre de la planta del trébol de tres hojas (o Trifolium).
Descripción
El nudo del trébol se puede definir como la curva obtenida de las siguientes ecuaciones paramétricas:
El (2,3)-nudo toroidal también es un nudo de trébol. Las siguientes ecuaciones paramétricas dan un (2,3)-nudo toroidal que se encuentra sobre un toro (geometría) :
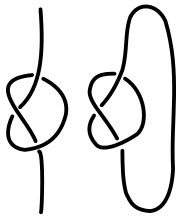

Cualquier deformación continua de la curva anterior también se considera un nudo de trébol. Específicamente cualquier curva isotópica a un nudo de trébol también se considera un trébol. Además la imagen especular de un nudo de trébol también se considera un trébol. En topología y teoría de nudos, el trébol se define usando un diagrama de nudos en lugar de una ecuación paramétrica explícita.
En geometría algebraica, el trébol también se puede obtener como la intersección en C2 de la unidad 3-esfera S3 con la curva compleja del plano de ceros del polinomio z2 + w3 (una parábola semicúbica).